Solving LeetCode Coin Change Problem for Data Science Interviews

Explore three different solutions to a difficult Python problem “LeetCode Coin Change Problem”

To maximize their chances of landing a job, beginner data scientists should learn a new skill.  Obviously, the knowledge of SQL is expected, but looking at job descriptions, you might’ve noticed that Python is one of the skills in particularly high demand.

Learning any new technical skill requires practice. Writing algorithms in Python is no exception. Fortunately, there are platforms like LeetCode and StrataScratch where you can practice common data science interview questions.

In this article, we will walk you through the solution to one of the most difficult interview questions called “LeetCode Coin Change Problem”.

LeetCode Coin Change Problem

In this question, we have a list of coin denominations and an amount of money. We have to find the fewest number of coins whose denominations add up to the specified amount. This LeetCode coin change question allows us to use each coin denomination as many times as we’d like.

Link to this LeetCode Coin Change Problem: https://leetcode.com/problems/coin-change/

Solving the LeetCode Coin Change Problem

When trying to solve a challenge on LeetCode, read the question description carefully. It usually includes important details and conditions of the question. In this case, the description says that coins can be reused as many times as needed.

Framework to Solve this LeetCode Coin Change Problem

This LeetCode coin change problem is one of the difficult problems that requires concentration and significant mental effort. Writing an algorithm is never easy, especially when you’re just getting started. Don’t be discouraged if the question seems confusing at first.

Take your time to fully understand the available data, expected output, constraints, and other important details of the question. Once you understand these components separately, you can put pieces together and see the fuller picture. Only then you can come up with a complete, efficient solution that handles any edge cases or variations in data.

1) Understand your data

• Before writing an algorithm to process it, look at its structure, format, and data types of available data.
• Read the description of the data. Pay attention to details like the uniqueness of each entry in the list and whether or not you can add coins multiple times.
• Consider the output of the algorithm and contrast it with available data. You might possibly need to transform or format values to return the right answer.
• Ensure that your answer is accurate for all possible inputs. Pay attention to the constraints of input data.

2) Formulate your approach

• Understand how available data and final answers relate to one another. Make a broad  plan of what you’ll need to do to process available data and get the answer.
• Think about what operations will be necessary to get the answer. In this case, your algorithm will have to repeatedly analyze values in the list to arrive at the answer.
• Consider your options. For this LeetCode coin change question, we have to choose between recursive and iterative approaches.
• Think of useful concepts and design patterns to find an answer. For this LeetCode coin change question, these are: base case, subproblems, backtracking.
• Try to implement a memory, so that your algorithm can ‘remember’ its progress.
• In the process of planning your approach, take notes. When focused on a problem, you might notice something important. Make sure to write it down to remember that detail. Writing down can also help you detect patterns and see connections between different approaches.
• Read the question and remember all conditions, including edge cases. Then go over your approach and make sure it's consistent for all inputs.

3) Code execution

• Define your algorithm and its structure. What arguments is it going to take?
• Plan how to turn your logical plan into a Python algorithm
• Decide how to persist the results of your checks to keep your algorithm efficient.
• See if your code would return the right answer for basic arguments. If not, see where it fails.
• Make sure to return the right value. For this LeetCode coin change question, we return the number of coins.

Difficult challenges like this one take time to digest. So the more time you spend with this question, the easier it will be to solve it.

Understand Your Data

Sometimes, looking at available data can be more helpful than reading about it. In the process of interview, candidates don’t always have the luxury of previewing available data. When possible, candidates should not miss out on the chance to look at available data.

All LeetCode challenges have at least three samples of available data. In some cases, samples also show the expected output and explanation behind the answer.

The answer to this LeetCode coin change problem depends on two variables: an array of coin denominations and the amount. In other words, we need to find the smallest number of integers that add up to the specified amount.

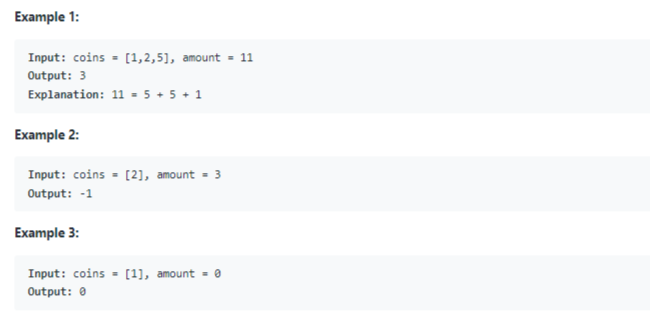
Some examples of data and expected output describe edge cases. In the picture above, example 2 describes the case when coin denominations can’t be added up to a certain amount.

Then we have an example where the amount is 0. In this case, the question specifies that the answer needs to be 0, because there are no coins needed to add up to that amount.

Constraints:

Inputs to the algorithm can be unpredictable. For this reason, LeetCode question descriptions also include information about constraints. These are clearly defined limitations of input data: the length of the coins array, the possible value of each coin, and the possible value of the amount.

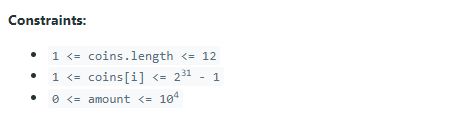
When writing an algorithm, it’s essential to consider these constraints. Your algorithm must return the right answer for any combination of inputs within the specified limits.

Solution 1:

This is a straightforward solution where we use a recursive function.

Formulate Your Approach

Start with a brute force approach to get your mind laser-focused on this challenge.

This challenge requires us to check multiple possible combinations of coins. Let’s imagine that we have three roads in front of us. Going down one path might lead us to another point where we have to make a choice between roads again.

Similarly, we will have to go through a possible combination of coins to find the one that:

1. Requires the fewest number of coins
2. Adds up to the specified amount

Essentially, we will be exploring the tree of choices. We can only get the final answer after we make a series of right choices. To do that, we will have to have a recursive function, which will explore our options and make the right choice.

Our recursive function needs to be designed in a way that it gradually arrives at the answer. Let’s go back to the road analogy. The body of the recursive function will help us choose the right road, considering the current situation.

Every time we call our recursive function, we will go down the right road, and we will be faced with a new choice. We will call the recursive function over and over until we reach the end and there are no more possibilities.

When we reach the end, we will either find the combination of coins that add up to the specified amount, or we will find that the current list of coins can not be added up to the amount. In this case, we are supposed to return -1.

The arguments for our recursive function need to have a starting point to know from which position to start exploring the options.

The easiest way to solve this challenge is to break down the problem into subproblems. In other words, let’s say our amount is 15, and the list of coins is [1,2,3,5].

If we have the answer for amount 10 (two 5 coins), it will be useful to store that answer so that we can use it when trying to find an answer for amount 15. In this case, answering the question for amount 10 would be a subproblem.

In our code, we will need to have the main function, which will store our progress towards the main problem. And we will have a recursive function, which is going to repeatedly call itself and explore coin combinations until it finds the right fit.

Code Execution

In our Solution class, we initialize a memory that will store the result of checking each subproblem. This way, we can avoid checking the same amount multiple times. We start with a base case and specify that amount 0 always requires 0 coins.

class Solution(object):
    def __init__(self):
        self.mem = {0: 0}
    
    def coinChange(self, coins, amount):
		coins.sort()
        minCoins = self.getMinCoins(coins, amount)
        
        if minCoins == float('inf'):
            return -1
        
        return minCoins
        
    def getMinCoins(self, coins, amount):
        if amount in self.mem:
            return self.mem[amount]
        
        minCoins = float('inf')
        
        for c in coins:
            if amount - c <  0:
				Break
				
			numCoins = self.getMinCoins(coins, amount - c) + 1
			minCoins = min(numCoins, minCoins)
        
        self.mem[amount] = minCoins
        
        return minCoins

First we define the main coinChange() function. It will take three arguments: self, coins, and amount. We use the self parameter to refer to the current instance of the class.

To keep things simple, we sort the list of denominations (coins parameter) in ascending order.

Then we define the getMinCoins() recursive function with two parameters: coins and amount. It will return the minCoins value, which represents the fewest number of coins that add up to the specified amount.

Within our recursive function, initially, we set the minCoins  variable to a high number. We will change its value if we can find any combination of coins that add up.

When we loop over coin denominations, first, we ensure that the amount argument supplied to the recursive function is not less than the coin denomination. If it is, we know that adding this coin will not get us the right answer.

In the for loop, we create a numCoins variable, which is going to store the minimum number of coins for this amount. It will call the recursive function with the difference between the amount perimeter and the current coin.

If the call to the recursive function finds a combination of coins, numCoins will store that number and one more for the coin we are currently using.

If the value of the numCoins variable was updated, we discard the default high number value of the minCoins variable and set it equal to the number of coins stored in numCoins.

Once we have found the minimum number of coins for a specific amount, we store the results in the memory. This helps us avoid unnecessary checks. In the recursive function, the first thing we do is to check if our memory already contains the answer for this amount. If it does, we skip making the calls to the recursive function.

In the main function, we check if minCoins is still set to the default high value. This tells us whether or not we were able to find a combination of coins that add up to the amount. If minCoins still has the default value, we return -1. If it’s not, then we return its value, which represents the minimum number of coins for this amount.

Solution 2:

Breadth-first approach to the problem.

Formulate Your Approach

In this approach, we will start from 0 and add coins until we reach the amount.

This is a slightly different and more efficient approach. Similar to the previous algorithm, we find an answer by breaking down the problem into subproblems. We will store our progress as a pair of two integers - the current amount and the minimum number of coins to reach that amount.

We will maintain a list of boolean values to represent which amounts were checked. This way, we can avoid unnecessary checks.

In this approach, we do not use a recursive function but a combination of while and for loops instead. We update a variable to store subproblems with their respective number of coins. We will end our check if we run out of subproblems, which means that there is no way to reach the amount. In this case, we will return -1.

Code Execution

As previously mentioned, in this solution, we are going to keep track of our progress as a pair of two values - the subproblem amount and the number of coins to reach it. For that, we import the deque value from the collections module.

from collections import deque


def coinChange2(self, coins: List[int], amount: int) -> int:
        if not amount:
            return 0

        queue = deque([(0, 0)])
        visited = [True] + [False] * amount
        while queue:
            totalCoins, currVal = queue.popleft()
            totalCoins += 1 
            for coin in coins:
                nextVal = currVal + coin
                if nextVal == amount: 
                    return totalCoins

                if nextVal < amount: 
                    if not visited[nextVal]: 
                        visited[nextVal] = True
                        queue.append((totalCoins, nextVal))

        return -1

We set the queue variable to a deque value, which is initially a pair of zeroes. This is our base case and means that for 0 amount, we should return 0 coins as the answer.

We start from this base case and gradually add coins to see if any combination allows us to reach the amount. As long as the queue variable stores a value, we will attempt to bridge the gap between the amount of the subproblem stored in the queue variable and the main amount.

We do this by taking current values in queue and storing them in two variables: totalCoins and currVal. Then we increment the totalCoins variable by one because we will attempt to add one more coin to get the amount.

If we get the amount, we will return the current number of coins. If we are unable to reach it, we update the visited list to indicate that we will try the sum of the previous amount and current coin.

We update the value of the queue variable, so next time it checks the updated amount and number of coins. The while loop will keep executing as long as the queue variable contains a pair of values to check.

Finally, we will either return the fewest number of coins or we will find that coins in the list can’t be added up to the specified amount and return -1.

Solution 3:

Solution based on principles of dynamic programming.

Formulate Your Approach

In this approach, we store answers to subproblems and store them in a list, which will have the same number of entries as the amount, plus one. Each entry will represent an amount from 0 to the specified amount parameter.

We add one extra item to the list because the first one will represent our base case - amount 0. The index of the first item will be 0, but its value should be 0 as well because the question tells us that the answer for this amount is 0.

The index of entries in the list is equal to the amount they represent. For example, the item on index 5 represents the subproblem where the amount is 5.

In our solution, we will loop over the coins list and try to find the minimum number of coins for each amount in the list.

Code Execution

First, we define a coinChange function that takes three arguments: self (an instance of a class), coins (a list of integers), and amount (an integer). Function outputs the number of coins necessary to reach the amount.

class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        dp = [float('inf')] * (amount + 1)
        dp[0] = 0
        
        for coin in coins:
            for i in range(coin, amount + 1):
                dp[i] = min(dp[i], dp[i - coin] + 1)
        return dp[amount] if dp[amount] != float('inf') else -1

In the body of the function, first we create a list of high integer values and store it in the dp variable. The amount parameter will determine the number of entries in the list. We will have as many entries as the amount, plus one. Each entry will be set to a high number. We can update their values later.

Each entry in the list represents the amount. If the amount is 10, we will have 11 items in the list. We will set dp[0] to 0. We do this to specify that for the amount 0, the number of coins will be 0 as well.

The item on index 1 will represent the number of coins for amount 1. The item on index 2 will represent the number of coins for amount 2. We continue to create items until we reach the amount.

The two nested for loops are the most important part of our function. We use them to go over denominations in the list and try to find solutions to subproblems between the coin denomination and the amount argument.

For example, if the coin is 5 and the amount is 10, we would have to check the minimum number of coins for 6, 7, 8, 9, and 10 amounts. We only check amounts that are higher than the coin. It would be pointless to check amounts less than the coin denomination.

As we progress towards finding the fewest number of coins to make up the amount, we can check if the current coin can be added up to previously checked subproblems to reach the amount. If we can add a current coin to previously checked subproblems, that takes us one step closer to finding the fewest number of coins for the amount.

If we can find a combination of coin denominations that add up to the amount, we will update the last item in the list. This entry represents the amount argument passed to the main function.

In the final line of the function, we return the value of the last entry, which represents the fewest number of coins for the amount.

Before we return it, we make sure that the last item in the list is not equal to its default value. If it is, we can assume that our for loops could not find coin denominations that add up to the amount. In this case, we must return -1.

Comparison of Approaches to Solve this LeetCode Coin Change Question

Three solutions share similarities, but there are important distinctions that affect their efficiency. The first approach uses a recursive function to find the answer. The latter two algorithms follow an iterative approach, relying only on while and for loops.

All three algorithms break down the problem into subproblems. We go through every possible combination of denominations until we determine the one with the fewest number of coins. If denominations in the list can’t be added up to the amount, we return -1. In all of them, we set up a base case for 0 amount.

All three algorithms store the answers to subproblems in their memory. This saves time because the algorithm doesn’t have to check the same subproblem multiple times.

As we mentioned, all three solutions maintain the memory of necessary coins for each subproblem from 1 to amount. We always initialize answers to a high number.

This is done to distinguish between cases when we can find an answer for each amount and when we can’t. If we can determine which coins add up to the amount, we will set the answer for that amount to the number of coins. If coins in the list can’t be added up to amount, we keep the initial value.

When we return the final answer for all three functions, we check if the initial value was updated. If not, we return -1.

Conclusion

These days, data scientists who are proficient in SQL, as well as Python, are in high demand. If you’re still new to Python, you might benefit from practicing more LeetCode questions like “Solving LeetCode Two Sum Problem” and “Solving LeetCode Word Break Problem”, and from reading blog posts like “Top 30 Python Interview Questions”.

Many data scientists know basic features of Python, but still can’t write efficient algorithms without extra practice. On StrataScratch, you can find and practice questions asked during interviews at the world’s biggest companies.