Binomial Distribution in Python for Coin Flip Prediction

Exploring the binomial distribution in Python: understanding probability calculations for coin flips with different methods.

In today’s article, we’ll show you how to apply statistics concepts, such as probability, in Python code. As a showcase, we’ll use the statistic interview question from Goldman Sachs and show you different ways to calculate the binomial distribution in Python.

We also made a video tutorial on the same topic (and the same question), so feel free to use it to make your life easier.

In this article, we will examine and solve the probability question asked by Goldman Sachs in an interview by using different approaches in Python.

Why Are Probability and Statistics Important in Data Science?

Probability and statistics are two branches of mathematics used extensively in data science.

Probability is the study of random events and the likelihood of them happening. It is used to model uncertainty in many real-world situations and is fundamental to statistical inference.

The study of data collection, analysis, and evaluation is called statistics. It includes using mathematical methods to summarize and draw conclusions from data.

Probability and statistics are used in data science to analyze data, make predictions, and inform decision-making. They are essential for understanding complex systems' behavior and identifying patterns and trends in data.

Probability Interview Question: Coin Flip Prediction

Link to the question: https://platform.stratascratch.com/technical/2407-21-unbiased-coins

Goldman Sachs is a global investment bank and provider of financial services, established in 1869. The company offers various financial services to corporations, governments, and individuals. It is one of the largest investment banks in the world and is headquartered in New York City.

This interview question asks you to determine the probability of getting an even number of heads when 21 unbiased coins are flipped.

An unbiased coin has a 50/50 chance of landing on either heads or tails.

When flipping multiple coins, possible outcomes can quickly become very large.

To solve this question, we need to use the concept of binomial distribution. Let’s see what it is.

Binomial Distribution in Python

The binomial distribution is a probability distribution that can be used to describe the number of successful or unsuccessful outcomes in a series of events, which must be independent of each other.

It is used when there are only two possible outcomes, like heads or tails, and the probability of success is the same for each trial.

The trials must meet two conditions:

1. They must have only two possible outcomes (heads or tails/success or failure),
2. The probability of success must be the same for each trial.
   

When flipping coins, success can be defined as getting heads, and failure can be defined as getting tails.

To find the probability of getting an even number of heads when flipping 21 coins, we need to calculate the probability of getting 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, or 20 heads.

We will do this by using the binomial distribution:

It means the following:

• P(X = k) – The probability of obtaining k successful outcomes in a total of n independent trials.
• n – The number of trials. (In this case, 21.)
• k – The number of successes. (In this case, heads.)
• p – The chance that a trial is successful. (In this case, 0.5)
• $\binom{n}{k} $ – The number of ways k successes can be chosen from a total of n independent trials.

Manual Calculation: Coin Flip Prediction

We can plug in the values and calculate the probability for each possible even number of heads.

Let’s first do it manually with the following values:

n = 21 (number of trials)
p = 0.5 (probability of success)
q = 1 - p = 0.5 (probability of failure)

Here’s the calculation

What is the meaning of these calculations? For instance, let’s look at P(18).

The formula means the probability of getting 18 heads when flipping a coin 21 times, which is 0,06341934204101562%. This is a little above 6 out of 10.000.

In the context of the interview question, when you flip 21 coins 10.000 times, you’ll probably get 18 heads six times.  It is a slim probability, as you see.

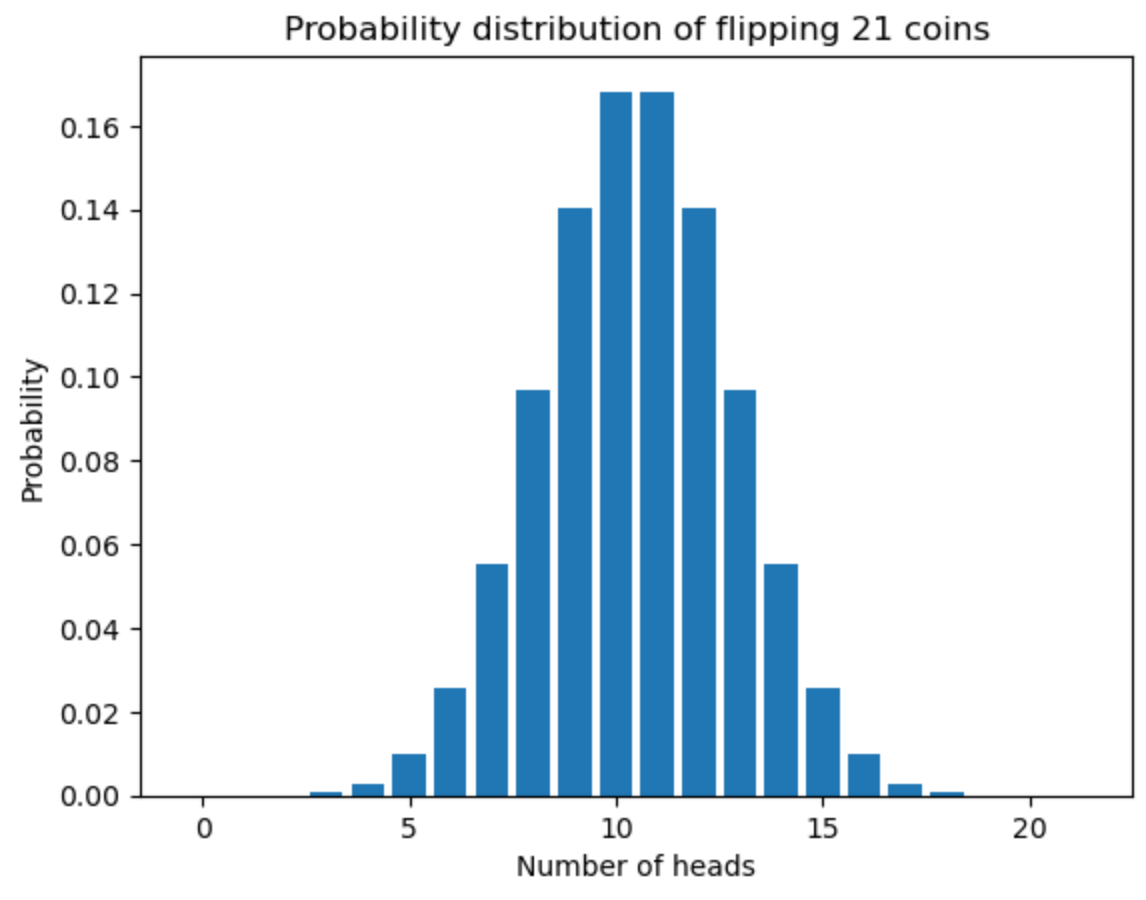
Here you can see the probability distribution of flipping 21 coins with an even number of heads based on our calculation.

To get the answer to the interview question, we need to add up all the probabilities:

Plug in all the individual probabilities we calculated and you get:

Now, let’s implement this calculation by using the math library in Python

Python Calculation: Coin Flip Prediction

Using the math Library

We can implement the binomial distribution of getting an even number of heads in 21 flips of unbiased coins using the math library in Python.

To do this, we can use a for loop to iterate over every even number of heads that can be obtained in 21 flips of an unbiased coin.

For each value of i in the range 0 to 22 (exclusive), with a step of 2, we can calculate the corresponding probability of getting i heads using the binomial distribution formula.

Inside the loop, we can first calculate the number of ways to choose i heads out of 21 flips using the math.comb() function.

We can then calculate the probability of getting exactly i heads in 21 flips of an unbiased coin, which is (1/2)**21. Finally, we can multiply the two values to obtain the probability of getting exactly i heads in 21 flips and store it in a list called probabilities.

We can use another for loop to print the probability of getting each even number of heads in the list probabilities.

After the loop finishes, we can compute the sum of all the probabilities stored in the list probabilities using the sum() function and print the total probability of getting an even number of heads in 21 flips.

Here's the code.

import math

# Create an empty list to store the probabilities of getting an even number of heads
probabilities = []

# Loop over all even numbers of heads that can be obtained in 21 flips
for i in range(0, 22, 2):
    # Calculate the number of ways to choose i heads out of 21 flips
    m = math.comb(21, i)
    # Calculate the probability of getting i heads in 21 flips
    n = (1/2 ** 21)
    prob = m * n 
    # Append the probability to the list
    probabilities.append(prob)

# Loop over the probabilities and print the probability of getting each even number of heads
for i, prob in enumerate(probabilities):
    print("The probability of getting {} heads in 21 flips is {}.".format(2*i, prob))

# Calculate the total probability 
total_prob = sum(probabilities)
print("Total probability of getting even number of heads is {}".format(total_prob))

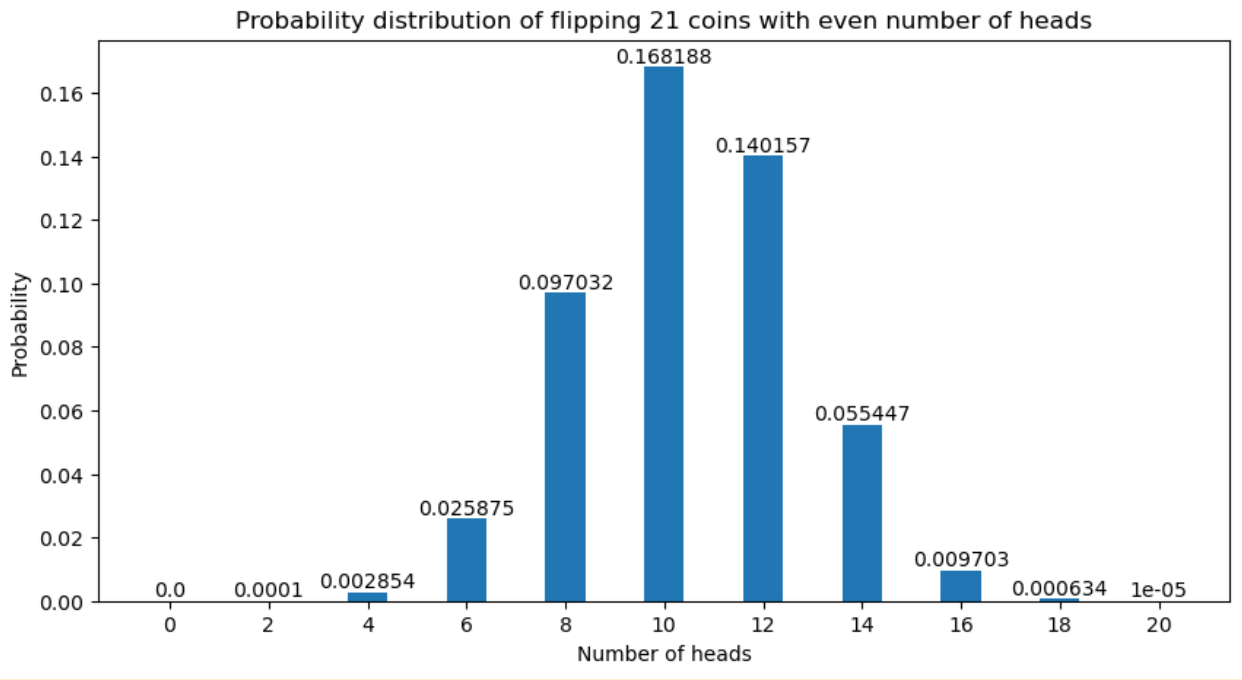
Now, let’s see the output.

In the earlier calculation, we manually calculated the probability of getting an even number of heads in 21 flips using the binomial distribution formula.

This involved calculating the probability of getting 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, and 20 heads separately, which can be time-consuming.

On the other hand, the code we just wrote using the math library allowed us to calculate all these probabilities in just a few lines of code.

This approach saves us a lot of time and effort, especially if we need to calculate the probabilities of getting more outcomes or if we need to repeat the calculation for a larger number of trials.

But we have one more way to implement this, and it’s even faster.

Using the SciPy Library

This time, we will use the pre-built function to calculate the probability.

In the following code, we first import the binom() function from the scipy.stats module.

We then define the binomial distribution with n trials and probability p of success using the binom() function.

We calculate the probability of getting an even number of heads (0, 2, 4, ..., 20) using the pmf() method of the binom distribution.

The pmf() method returns the probability mass function (PMF) of the distribution for each value in the given range.

We then use another for loop to print the probability of getting each even number of heads in the list even_probs.

Finally, we calculate the total probability of getting an even number of heads in 21 flips by summing up the probabilities in the list even_probs.

Using the scipy library to calculate the binomial distribution provides a more efficient and convenient calculation method. It allows us to define and calculate the distribution in just a few lines of code.

Here is the code.

from scipy.stats import binom

n = 21
p = 0.5

# Define the binomial distribution with n trials and probability p of success
binom_dist = binom(n, p)

# Calculate the probability of getting an even number of heads (0, 2, 4, ..., 20)
even_probs = binom_dist.pmf(range(0, 22, 2))

# Print the probability of getting each even number of heads
for i, prob in enumerate(even_probs):
    print("The probability of getting {} heads in 21 flips is {}".format(2*i,prob))

# Calculate the total
total_prob = sum(even_probs)
print("Total probability of getting even number of heads is {}".format(total_prob))

Here is the output.

If you compare the results obtained from the two Python methods, you may notice that they are not exactly the same.

Why are the Results (Slightly) Different?

The difference between the SciPy and math calculations is due to floating-point precision errors.

In computer programming, floating-point numbers are represented in a limited number of bits, which can cause a loss of precision when performing calculations.

This is why we are getting slightly different values for the probabilities of getting an even number of heads when comparing the results of the two methods.

Both methods provide a good approximation of the true probability, and the difference between the two is negligible for most practical purposes.

If you work on longer scripts and plan to make longer calculations, plus you have limited computational power, working with SciPy is more efficient and faster.

Yet, if you have enough resources, we would recommend the first calculation where we used math. This is if you want to be sure about the results, even if these slight differences made little difference.

If you want to minimize the impact of floating-point errors, you can round the results of the calculations to the desired precision.

Here is the code.

total_prob = round(total_prob, 14)
print("Total probability of getting even number of heads, after correcting precision error is {}".format(total_prob))

Here is the output.

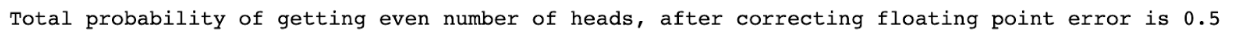
Conclusion

In this article, we explored a statistic question from Goldman Sachs and answered it by using  Python.

We went through different approaches and explained each step in detail. Also, we did implement it by using a pre-built function.

Overall, this article is an excellent example of how binomial distribution can be solved manually or using Python.

If you want to master the random variables and probability distributions and crack your next Data Science Interview, check out our post “Random Variables and Probability Distributions”.