Commonly Asked Data Structure Interview Questions

Categories:
 Written by:
Written by:Nathan Rosidi
Data structure interview questions are a big part of interviews for many data roles. To answer them, you should know the data structures we’ll cover here.
The first step in understanding data algorithms is understanding data structures, which are algorithms’ building blocks.
They are vital in implementing and optimizing algorithm performance. Data structures’ importance is reflected in the knowledge about them being regularly tested in interviews where algorithms are a required skill.
In this article, we will explain different data structures and solve one actual interview question for each.
Understanding Algorithms and Data Structures
An algorithm is a step-by-step sequence of instructions whose purpose is to perform a specific task or solve a problem. It takes these instructions and applies them to inputs to produce outputs.
Some examples of what these tasks and problems might be are data sorting, finding the shortest path in a network, searching for an item in a dataset, data processing, automation of various repetitive tasks (e.g., sending emails or inventory management), optimization (e.g., optimizing search engine results or network performance), or use in artificial intelligence and machine learning (e.g., recommendation systems or voice recognition).
A data structure is a specialized format for organizing and storing data. There are many different data structures, each with its own characteristics and uses, which we’ll discuss in a heap, pun intended.
Why are data structures important for algorithms? Different data structures store, retrieve, and manipulate data differently during the algorithm execution. Because of that, data structures are crucial in optimizing algorithms.
Different Data Structures Explained
In the following sections, I will explain these data structures.

The explanations will be followed by solving the actual data structure interview questions you could encounter at your job interview.
Since we’ll write algorithms in Python, it’d be helpful if you’re familiar with data structures in Python.
Arrays
Definition: Arrays are linear collections of elements. Each element is identified by an index. Arrays are zero-indexed, meaning that the first element in an array is always 0, the second is 1, and so on.
Illustration:
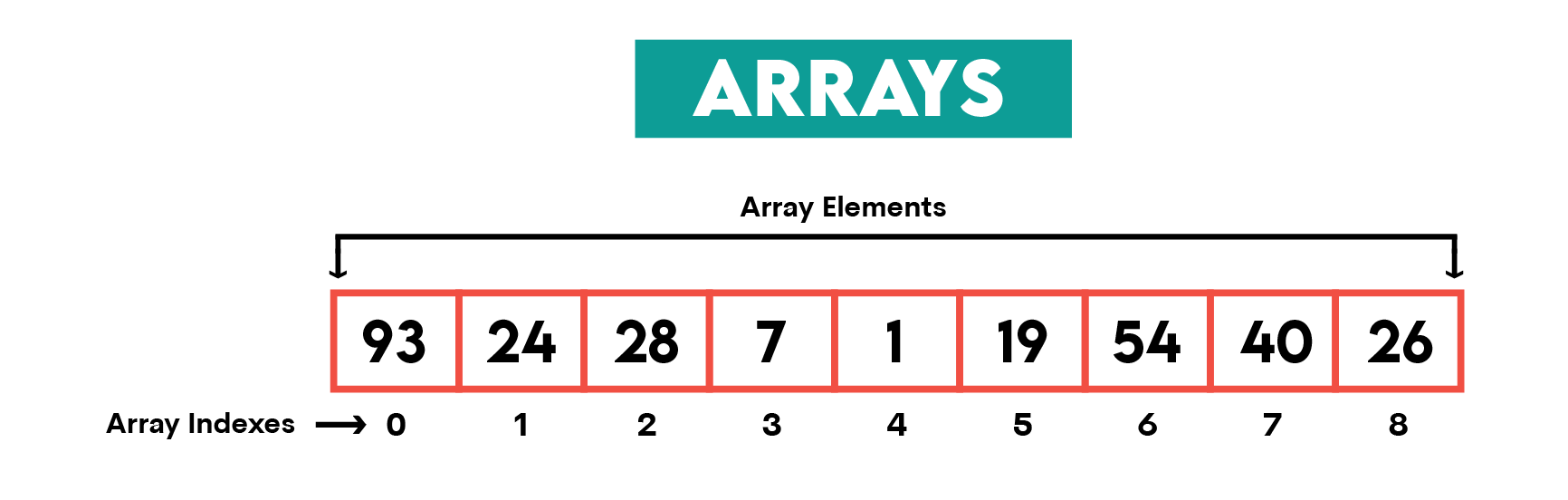
Typical Use Examples:
- Student grades: [90, 77, 100, 69]
- Representing a chessboard (an example shows the first two rows of 8x8 grid): [[0, 1, 0, 1, 0, 1, 0, 1], [1, 0, 1, 0, 1, 0, 1, 0], …]
- Inventory counts: [130, 120, 100, 55]
Pros: Arrays' two main pros are that they are simple to implement and use and that their indexes allow fast access to elements (O(1) time complexity).
Cons: For the fixed-size arrays, one significant con is that they can’t be dynamically resized.
Due to that, another con is that insertion and deletion of data can be costly (O(n) time complexity). The second con is only partially valid for dynamic arrays; it applies only to inserting data in the middle or resizing. However, when appending data at the end, the time complexity is O(1) for dynamic arrays.
Data Structure Interview Questions: Arrays
One of the popular interview questions involving arrays is to find the largest value in the array, such as in this question by Twitter.
Link to the question: https://platform.stratascratch.com/algorithms/10431-maximum-number-in-array
We can have this array to test the algorithm (Test 1): [3, -2, 7, 3, -9, 12]
The algorithm written in Python is this.
def find_largest_number(arr):
largest = arr[0]
for num in arr:
if num > largest:
largest = num
return largest;
The code defines the find_largest_number function, with arr as its parameter. It then creates a base case largest = arr[0], which makes the first array element a starting point for value comparison; it is considered the largest value until larger is found.
The for loop goes through each number num and compares it to the largest value. If the condition num > largest is true, then we’ve found the new largest value. After going through each array element, the algorithm outputs the largest value.
Test it on the example array above, and you’ll get this output.
Expected Output
Official output:
12Official output:
-3Official output:
1000000Strings
Definition: A string is primarily a data type but can also be seen as a data structure, as it’s implemented in arrays or lists. It’s a sequence of characters, and it stores data as text. Several typical operations are performed on strings, such as concatenation, searching, and slicing.
Illustration:
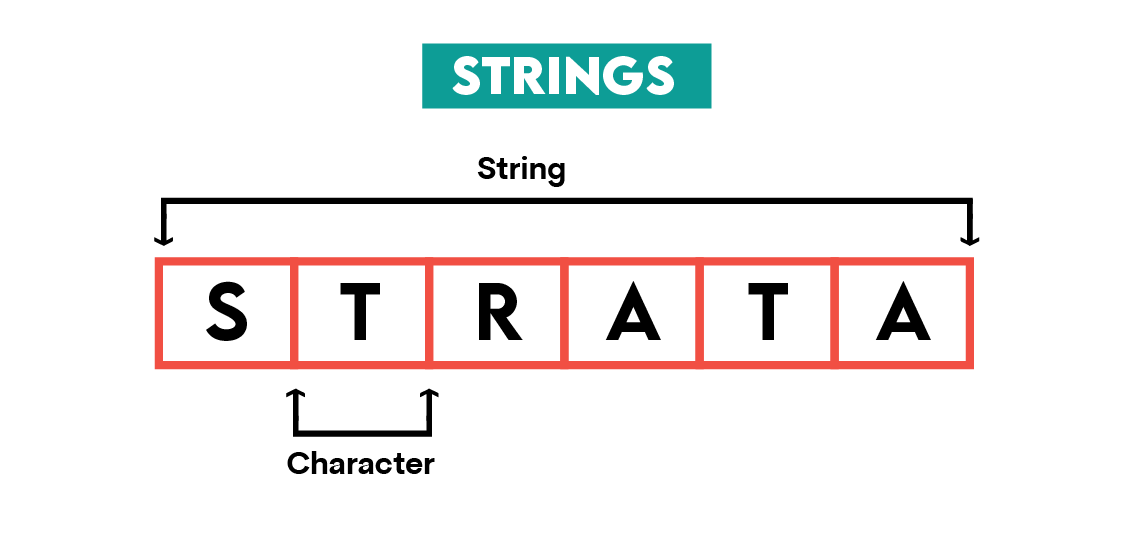
Typical Use Examples:
- Sentence: 'Dancing llamas love disco'
- DNA sequence: 'AGCTGAC'
- Username: 'JohnnyC123
Pros: Strings are immutable in many programming languages, which can be useful when you want to prevent unintended modification.
Strings also come with a rich set of manipulation and comparison operations, such as concatenation, substring extraction, pattern matching, trimming, case conversion, and comparison. These operations make handling and manipulating textual data quite simple.
Cons: If the strings are immutable, some operations, such as concatenation, can be computationally expensive. Concatenation, in this case, doesn’t change the existing string but creates a new one, which involves memory allocation and copying the existing strings.
In some programming languages, strings may have a fixed length. This often results in allocating a maximum possible size for strings in advance, which could mean there’s a lot of wasted memory not used sufficiently.
For more information, read our article about working with strings in Python.
Data Structure Interview Questions: Strings
The interview question by EY asks you to perform a common task using an algorithm: sort a string alphabetically.
Link to the question: https://platform.stratascratch.com/algorithms/10407-alphabetize-strings
Here’s the question solution.
def sort_string(string):
return ''.join(sorted(string));
In the first line of code, we define the sort_string function with the parameter string, which is the input string we want to get sorted.
Next, we use Python’s built-in function sorted to sort the string. This function’s output will be a list of characters sorted alphabetically.
Finally, we use join to concatenate the sorted list of characters into a single string. The characters will be joined without any separator, as indicated by '' before .join.
Here’s the algorithm output if run on the following string (Test 2): "escapevelocity".
Expected Output
Official output:
"abcdxyz"Official output:
"aceceilopstvye"Official output:
"PRchknoosty"Linked Lists
Definition: Linked lists are linear data structures consisting of nodes. Each node contains a data part and a pointer or reference (depending on the programming language) that leads to the next node.
Illustration:

Typical Use Examples:
- Playlist: each song points to the next one
- Dynamic data: messages in a chat stored as the conversation progresses
- Task list: tasks are added and removed as needed
Pros: Linked lists are dynamic data structures that easily grow and shrink, which makes them ideal for regularly changing data.
Along with that comes the ease with which data is inserted or deleted.
Cons: Linked list searches are slower than in arrays, for example. To access data at a specific position, the linked list must be traversed from its beginning, following each pointer until the desired data is reached. This indirect access to data through the index has a time complexity of O(n); n is the number of elements in the linked list.
Another linked list con is memory requirement since they contain not only data but a pointer to the next node. Required memory could be significant for large linked lists.
Data Structure Interview Questions: Linked Lists
The interview question by Goldman Sachs asks you to remove all duplicate elements from an unordered linked list in one traversal.
Given an unordered singly linked list, remove all duplicate values such that only the first occurrence of each element remains. The operation must be performed in a single traversal of the list using a set to track seen values.
The list should retain the original order of first occurrences. Return the modified linked list as a Python list.
Link to the question: https://platform.stratascratch.com/algorithms/10389-unique-elements-in-unordered-linked-list
To write this algorithm, you need to define the remove_duplicates_from_linked_list function, which specifies the whole process of removing duplicates from a linked list.
Every time a new node is created, the __init__ method is called to set up the data (the value of the node) and next (a pointer to the next node).
Next, the create_linked_list function. It takes a list of values and creates a linked list by creating the first node from the first value. It then goes through the rest of the values and creates new nodes linked to each other.
After the duplicates are removed (by the function explained below), the linked list is converted back to a list by iterating through the nodes and collecting their values.
The remove_duplicates function uses Python’s set seen to track the values that have already been encountered in the linked list (duplicates). If it’s a duplicate, the function skips it and goes to the next node. If it’s not a duplicate, the value is added to the set, and the function moves to the following node. It checks all nodes that way and, by doing so, removes duplicates.
In the last three lines of the code, the process is defined in the following way:
- The input list is converted into a linked list
- Duplicate nodes are removed from the linked list
- The linked list is converted back into a Python list
Here’s the code.
def remove_duplicates_from_linked_list(input_list):
class Node:
def __init__(self, data):
self.data = data
self.next = None
def create_linked_list(values):
if not values:
return None
head = Node(values[0])
current = head
for value in values[1:]:
current.next = Node(value)
current = current.next
return head
def linked_list_to_list(head):
result = []
current = head
while current:
result.append(current.data)
current = current.next
return result
def remove_duplicates(head):
if head is None:
return head
current = head
seen = set([current.data])
while current.next:
if current.next.data in seen:
current.next = current.next.next
else:
seen.add(current.next.data)
current = current.next
return head
head = create_linked_list(input_list)
head = remove_duplicates(head)
return linked_list_to_list(head);
Testing the algorithm on the following data (Test 3) returns the following result.
Expected Output
Official output:
[1, 2, 3]Official output:
[5]Official output:
[]Official output:
["a", "b", "c"]Stacks
Definition: Stacks are linear data structures that follow the LIFO method – Last In, First Out. It relates to the order in which data is added to and removed from a stack. So, in other words, the last added element will be the one to be removed first to access data in the middle or at the bottom.
Three main operations connected with the stacks are:
- Push – adds an element to the top of a stack
- Pop – removes and returns an element from the top of a stack
- Peek – returns the value of the top element without removing it, i.e., like pop without modifying a stack
Illustration:
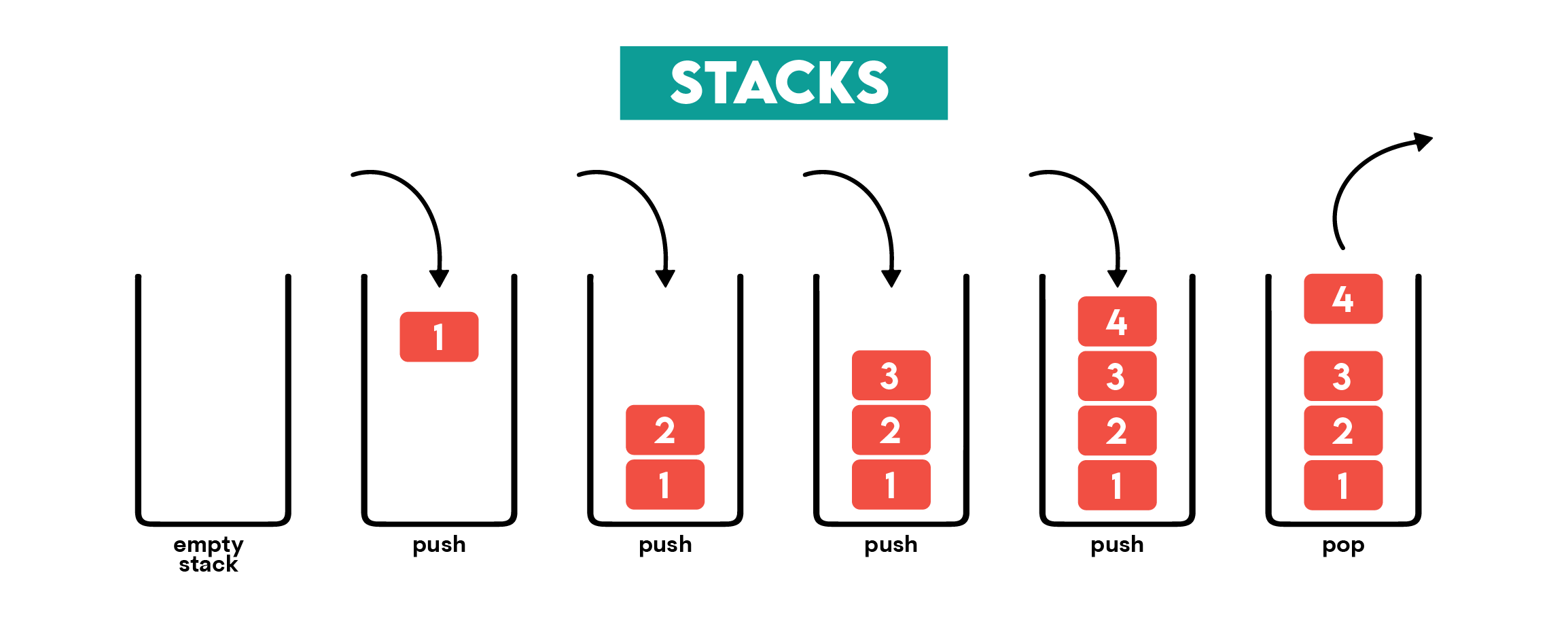
Typical Use Examples: Stacks are used for tasks that require reversing, for example:
- Undoing functionality in text editors
- Evaluating mathematical expressions, e.g., in reverse Polish notation
- Navigating back in a web browser
Pros: Due to their characteristics, stacks are efficient in managing function calls, parsing, and backtracking.
They are also very adaptable since they’re easy to implement in arrays, linked lists, or dynamic arrays.
Cons: Their pro – the LIFO principle – is also a con when you want random access to elements. This would require removing all the elements from the top to reach if the required element is not on the top of the stack, which is not very efficient.
It limits their use cases, making them unsuitable for scenarios where frequent searches are required.
Data Structure Interview Questions: Stacks
The Amazon interview question requires you to know how to work with stacks and implement them using a linked list.
Link to the question: https://platform.stratascratch.com/algorithms/10436-linked-list-stack
Whichever of the three input data you’re using, the task remains the same: process specified data and perform a series of operations.
For example, the Test 1 input is {"values": [1, 2, 3], "operations": ["push", "push", "push", "pop", "pop", "peek"]}. It checks the stack operations by pushing three elements and then popping two elements, followed by peeking the top element.
Let’s write the algorithm to do that.
We first define the Node class, followed by the Stack class. In the Node class, data holds the node value, and next points to the following node in the stack. The head attribute in the Stack class indicates the top of the stack.
The code then defines four functions. The first function, __init__, checks if the stack is empty.
The second function is push, which adds a new node with the provided data and adds it to the top of the stack. The next pointer of this new node is set to the current head, which is the current top of the stack. The head is updated to point to this new node, making it the new top of the stack.
The next function is pop. It checks if the stack is empty, removes the top node from the stack, and outputs its value.
The fourth function is peek. It, too, first checks if the node is empty and then returns the data of the top node without removing it from the stack.
The purpose of the process_operations method defined within the Stack class is to process all the functions we mentioned above based on provided inputs and return the results of the pop and peek operations in an ordered list.
The values and operations from the input data are retrieved using the get() method. Finally, the stack_instance is initialized, and the process_operations method is called to execute the stack operations.
def create_stack(input_data):
class Node:
def __init__(self, data):
self.data = data
self.next = None
class Stack:
def __init__(self):
self.head = None
def is_empty(self):
return self.head is None
def push(self, data):
new_node = Node(data)
new_node.next = self.head
self.head = new_node
def pop(self):
if self.is_empty():
return None
popped_node = self.head
self.head = self.head.next
popped_node.next = None
return popped_node.data
def peek(self):
if self.is_empty():
return None
return self.head.data
def process_operations(self, values, operations):
output = []
value_index = 0
for operation in operations:
if operation == "push" and value_index < len(values):
self.push(values[value_index])
value_index += 1
elif operation == "pop":
result = self.pop()
if result is not None:
output.append(result)
elif operation == "peek":
result = self.peek()
if result is not None:
output.append(result)
return output
values = input_data.get('values', [])
operations = input_data.get('operations', [])
stack_instance = Stack()
return stack_instance.process_operations(values, operations);
Executing this algorithm on the Test 1 input returns the following output.
Expected Output
Official output:
[3, 2, 1]Official output:
[5, 6]Official output:
[7, 9]Queues
Definition: Queues are, too, linear data structures. Unlike stacks, queues follow the First-In-First-Out (FIFO) principle for adding and removing data. This means that the first element added to the queue is the first one to be removed from the queue.
Unlike in stacks, elements in queues are not stacked on top of each other but lined one after the other. Based on this, the operations characteristic for queues are:
- Enqueue – adds an element to the end (rear) of the queue
- Dequeue – removes and returns an element from the front (head) of the queue
- Peek – returns an element from the front (head) of the queue without removing it
- Empty – checks whether the queue is empty
- Full – checks whether the queue is full
Illustration:
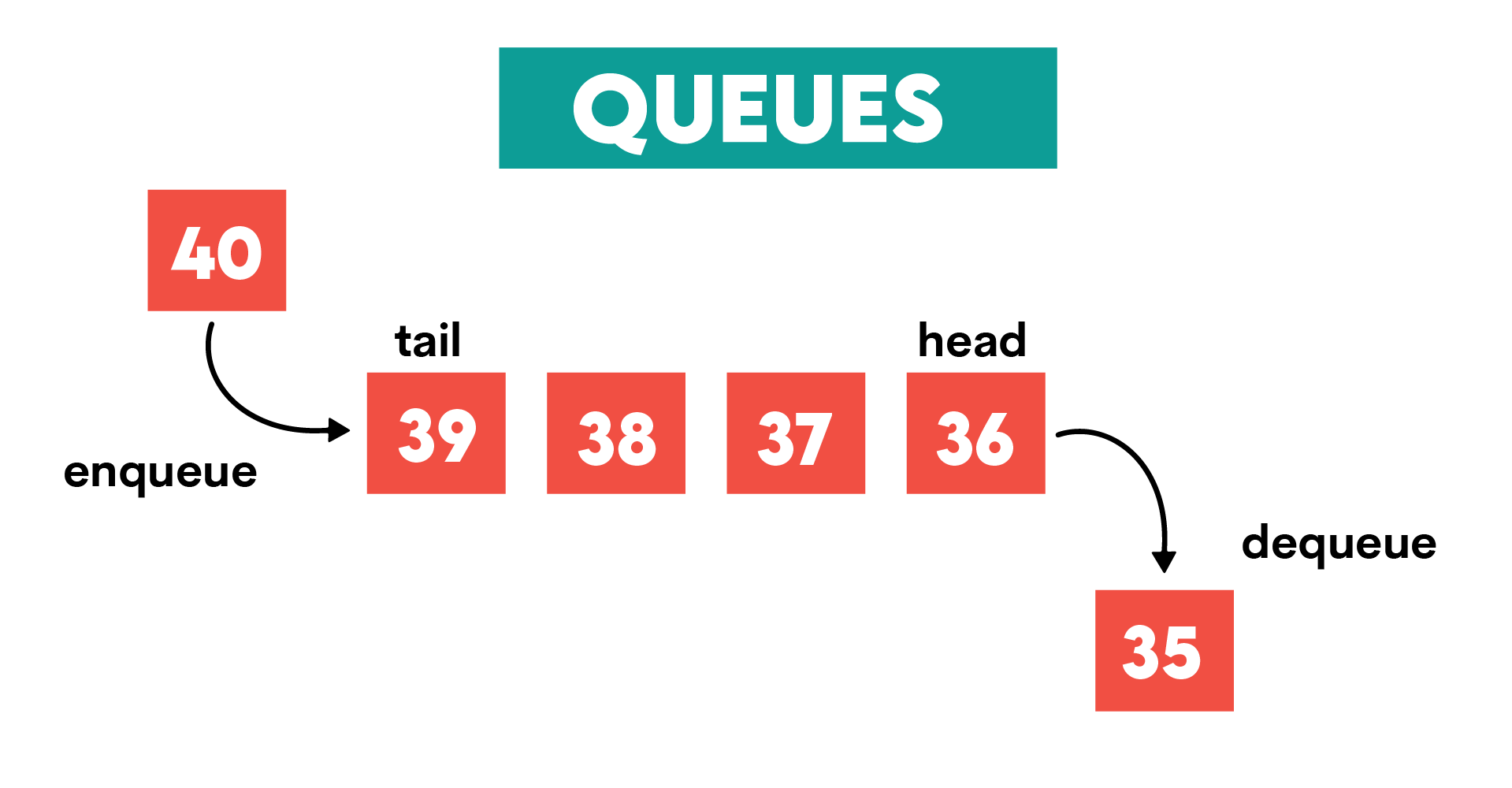
Typical Use Examples: Queues are primarily used in scheduling tasks such as:
- CPU tasks
- Printer tasks where jobs are executed in the order they are received
- Handling customer service requests in the order they arrive
Pros: The queues’ characteristics ensure fair and orderly access to the element, where every element waits its turn to be processed.
This makes them ideal for task scheduling and management, as they allow sequential processing.
Cons: Their fair and orderly data processing is also a con because elements not at the front of the queue can’t be accessed directly; all preceding elements must be dequeued first. This could lead to inefficient data processing and is not suitable for random access.
Data Structure Interview Questions: Queues
Since we don’t have a data structure interview question that uses queues, we will reuse the previous question, in which we worked with stacks.
Link to the question: https://platform.stratascratch.com/algorithms/10436-linked-list-stack
The same algorithm can be adapted to process queues. Imagine we have this as an input: {"values": [1, 2, 3], "operations": ["enqueue", "enqueue", "enqueue", "dequeue", "dequeue", "peek"]}.
As you can see, the input is similar to what we had earlier. However, as we are now using a queue data structure; there is enqueuing and dequeuing instead of push and pop.
The rewritten algorithm is this.
def create_queue(input_data):
class Node:
def __init__(self, data):
self.data = data
self.next = None
class Queue:
def __init__(self):
self.front = None
self.rear = None
def is_empty(self):
return self.front is None
def enqueue(self, data):
new_node = Node(data)
if self.rear is None:
self.front = self.rear = new_node
else:
self.rear.next = new_node
self.rear = new_node
def dequeue(self):
if self.is_empty():
return None
dequeued_node = self.front
self.front = self.front.next
if self.front is None:
self.rear = None
dequeued_node.next = None
return dequeued_node.data
def peek(self):
if self.is_empty():
return None
return self.front.data
def process_operations(self, values, operations):
output = []
value_index = 0
for operation in operations:
if operation == "enqueue" and value_index < len(values):
self.enqueue(values[value_index])
value_index += 1
elif operation == "dequeue":
result = self.dequeue()
if result is not None:
output.append(result)
elif operation == "peek":
result = self.peek()
if result is not None:
output.append(result)
return output
values = input_data.get('values', [])
operations = input_data.get('operations', [])
queue_instance = Queue()
return queue_instance.process_operations(values, operations)
input_data = {"values": [1, 2, 3], "operations": ["enqueue", "enqueue", "enqueue", "dequeue", "dequeue", "peek"]}
output = create_queue(input_data)
print(output);
There are two main differences from the algorithm that uses stacks. First, two defined operations are enqueue and dequeue, not push and pop.
Second, we can’t run this code in the question’s code editor, as its input data are stacks. So, we have to run it in, for example, Jupyter Notebook. Because of that, the algorithm code has to be amended at the end to define the input data.
Let’s run it and see if the changes work. They do, as we got the same output!
Trees
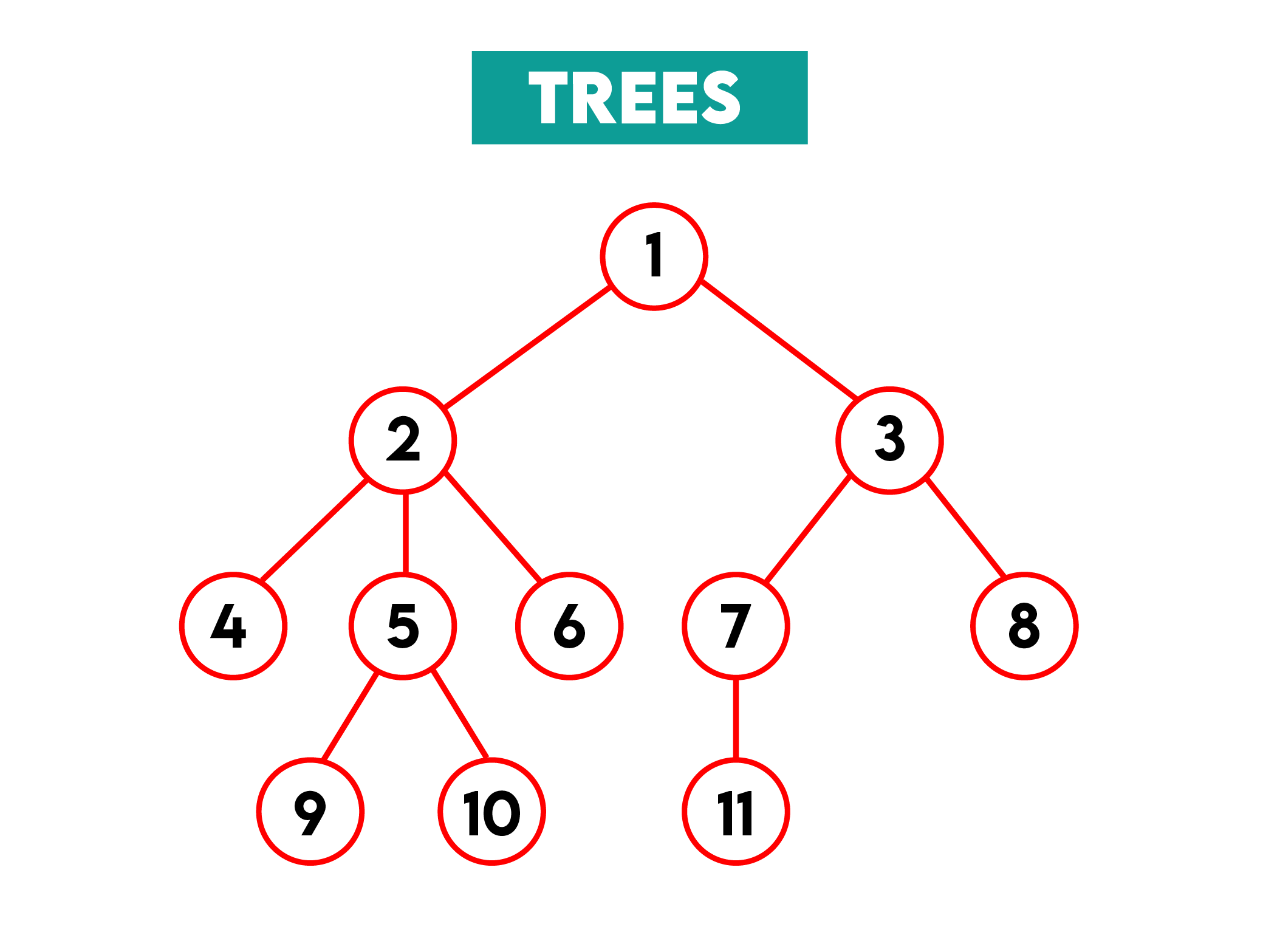
Definition: A tree is a hierarchical data structure where each node holds a value and can be connected to many children nodes. There are several types of trees, with a binary tree (each node has at most two children) being the most commonly used.
Illustration:
Typical Use Examples:
- A file system, all with directories and files
- Search algorithms, e.g., binary search trees
- Organizational charts
Pros: Since trees are inherently hierarchical data structures, they are – as expected – perfect for representing hierarchical data. Due to their consisting of nodes, traversing hierarchical data becomes easy.
A special type of tree structure called a balanced tree, such as an AVL tree or a Red-Black tree, keeps its height in check. This makes it efficient, which is great for processing large amounts of data, as the operations are performed in O(log n) time, where n is the number of nodes.
Cons: Of course, if a tree becomes unbalanced, then it’s a con. In other words, the tree becomes inefficient, where operations could degrade to being performed in O(n) time complexity.
Another con is that trees are not easy to implement, as they require complex algorithms that must handle pointers and maintain tree integrity.
Data Structure Interview Questions: Trees
This data structure interview question by Meta asks you to find the maximum path-sum of any non-empty path, given a tree root and several constraints.
Link to the question: https://platform.stratascratch.com/algorithms/10429-maximum-path-sum-in-tree
In this question, we’re dealing with a binary tree. It means that each node contains a value, a reference to a left child node, and a reference to a right child node.
We will test the algorithm using this input (Test 2): [-10, 9, 20, null, null, 15, 7]. In this problem, a binary tree is represented as a list, where the 0th index represents the root node. A left child node is at the index 2*index +1, and the right child node is at the index 2*index + 2, where index is the index of the current node in the list.
To write the algorithm, you first need to understand that the maximum path sum in a binary tree is the maximum of:
- The node’s value
- The node's value plus the maximum path sum of its left subtree
- The node's value plus the maximum path sum of its right subtree
- The node's value plus the maximum path sums of both its left and right subtrees
So, here’s the algorithm.
def max_path_sum_solution(tree_data):
class tree_node:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class solution:
def __init__(self):
self.max_sum = float('-inf')
def max_path_sum(self, root: tree_node) -> int:
def max_gain(node):
if not node:
return 0
left_gain = max(max_gain(node.left), 0)
right_gain = max(max_gain(node.right), 0)
current_sum = node.val + left_gain + right_gain
self.max_sum = max(self.max_sum, current_sum)
return node.val + max(left_gain, right_gain)
max_gain(root)
return self.max_sum
def list_to_tree(lst, idx=0):
if idx < len(lst) and lst[idx] is not None:
node = tree_node(lst[idx])
node.left = list_to_tree(lst, 2 * idx + 1)
node.right = list_to_tree(lst, 2 * idx + 2)
return node
return None
root = list_to_tree(tree_data)
solution_instance = solution()
return solution_instance.max_path_sum(root);
Let’s break down this code. The tree_node class is defined to define the structure of the nodes in the binary tree.
Then, another class is defined, namely solution, which finds the maximum path sum in the binary tree. It does that using max_sum for the maximum path sum so far and max_path_sum to calculate the maximum path sum for the entire tree, starting from the root node.
The max_gain recursive method finds the maximum path sum (gain) that could be obtained from the current node and going down to any of its children, ensuring that negative sums are not considered (this is done by comparing against 0 using max). It then updates the global max_sum with the current sum if it’s larger than the previously saved max_sum.
The list_to_tree function converts a binary tree represented as a list into an actual binary tree data structure.
After all that, we can define the main max_path_sum_solution function. It ties together all the earlier steps.
Here’s the algorithm’s update used on the Test 2 input.
Expected Output
Official output:
6Official output:
42Official output:
2Graphs
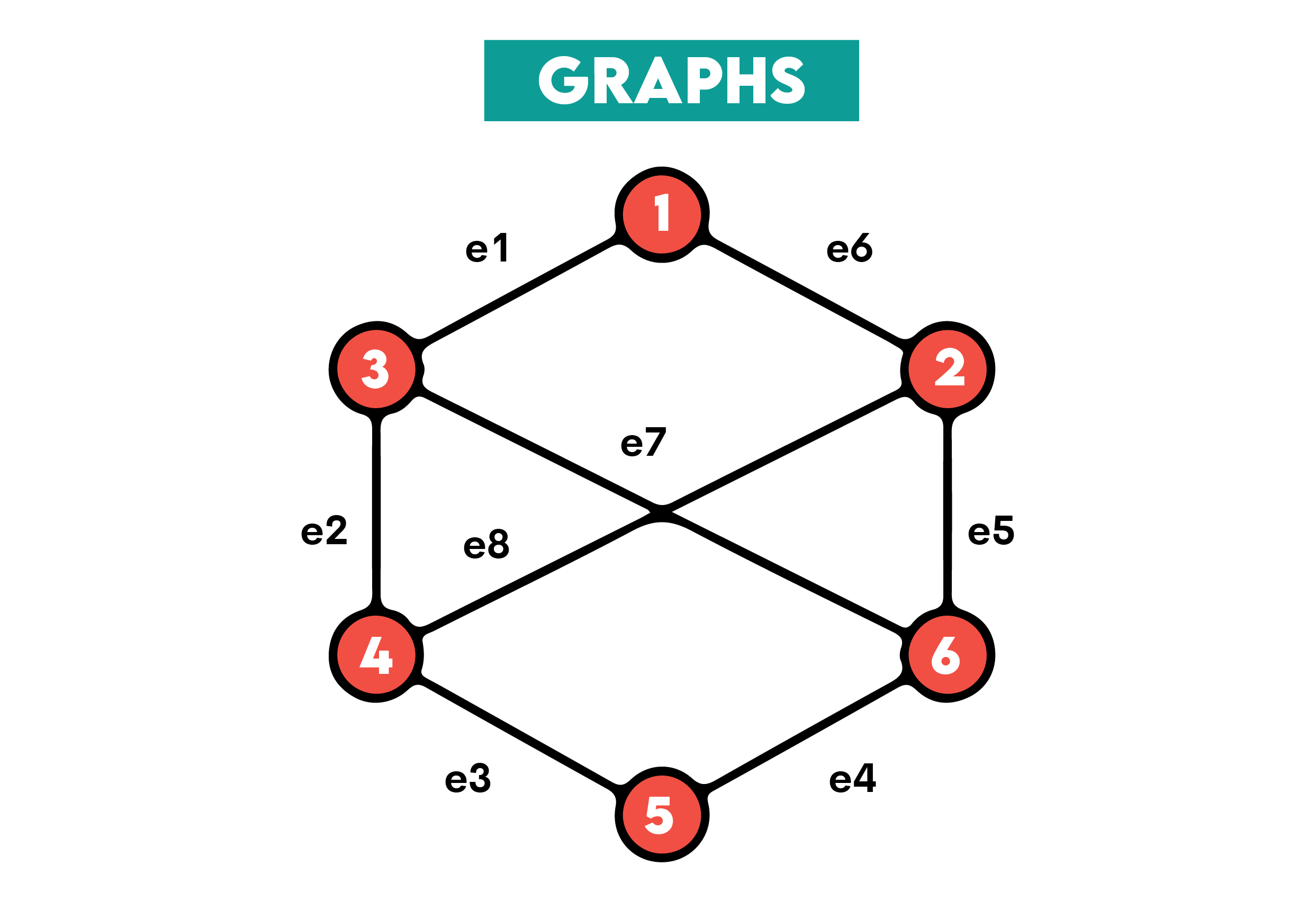
Definition: A graph is a data structure consisting of nodes or vertices. This might seem similar to trees and, indeed, trees are a specialized type of graph. To be more specific, a hierarchical and more rigid kind of graph.
Graphs don’t have a root node, the relationships between nodes are arbitrary, and each node possibly has any number of edges, i.e., connections to other nodes.
Illustration:
Typical Use Examples:
- Social networks – users as nodes, friendships as edges
- Road maps – intersections as nodes, roads as edges
- Project management – managing dependencies in PERT charts
Pros: Graph’s nonlinear nature makes them flexible and suitable for representing complex and multiple relationships between entities, with examples given above.
Graphs also support various traversal algorithms, for example, Depth-First Search (DFS) and Breadth-First Search (BFS), which are used in exploring a graph’s nodes and edges.
Cons: Their complexity makes graphs memory-intensive. For example, representing a graph using adjacency matrices requires O(V2) space, with V being the number of vertices.
In addition, performing operations on graphs requires complex algorithms. Examples of such operations include finding the shortest path in weighted graphs (Dijkstra’s algorithm), detecting cycles, graph coloring, network flow, and finding the minimum spanning tree.
Data Structure Interview Questions: Graphs
The interview question by Microsoft tests your graph knowledge. To be more specific, bipartite graph knowledge.
Determine if a graph is bipartite, given a list of its edges in form (u, v).
Link to the question: https://platform.stratascratch.com/algorithms/10399-bipartite-graph-detection
The task here is to determine if a graph is bipartite, given a list of its edges in form (u, v), a list of tuples.
To solve this problem, you must know that a bipartite graph is one in which the set of vertices can be divided into two disjoint sets so that every edge connects a vertex in one set to one in the other set.
The first part of our algorithm constructs a graph by initializing an empty dictionary graph. This function goes through the input, adding nodes to the graph if they don't already exist and appending each node to its corresponding neighbors' list, which is converted to a graph structure.
Then, we create an empty dictionary color, which will be used to keep track of the color assigned to each node.
Next, we use Depth-First Search (DFS) and coloring to determine if the graph is bipartite by trying to color every node and all its connected nodes in a bipartite manner. This means assigning a color to a node (0 or 1) and then trying to assign the opposite color (1 or 0) to each neighboring node. If a neighboring node is already colored and the color is not the opposite color, the function will return False, which means the graph is not bipartite.
The function iterates through all nodes, and if all nodes are successfully colored, it will return True, indicating that the graph is bipartite.
def is_bipartite(edges):
graph = {}
for u, v in edges:
if u not in graph:
graph[u] = []
if v not in graph:
graph[v] = []
graph[u].append(v)
graph[v].append(u)
colors = {}
def dfs(node, color):
if node in colors:
return colors[node] == color
colors[node] = color
for neighbor in graph[node]:
if not dfs(neighbor, 1 - color):
return False
return True
for node in graph:
if node not in colors:
if not dfs(node, 0):
return False
return True;
If we apply the above code to the Test 1 input, which is [[1, 2], [2, 3], [3, 4], [4, 1], [1, 3]], the output says the graph is not bipartite.
Expected Output
Official output:
falseOfficial output:
trueOfficial output:
falseHash Tables
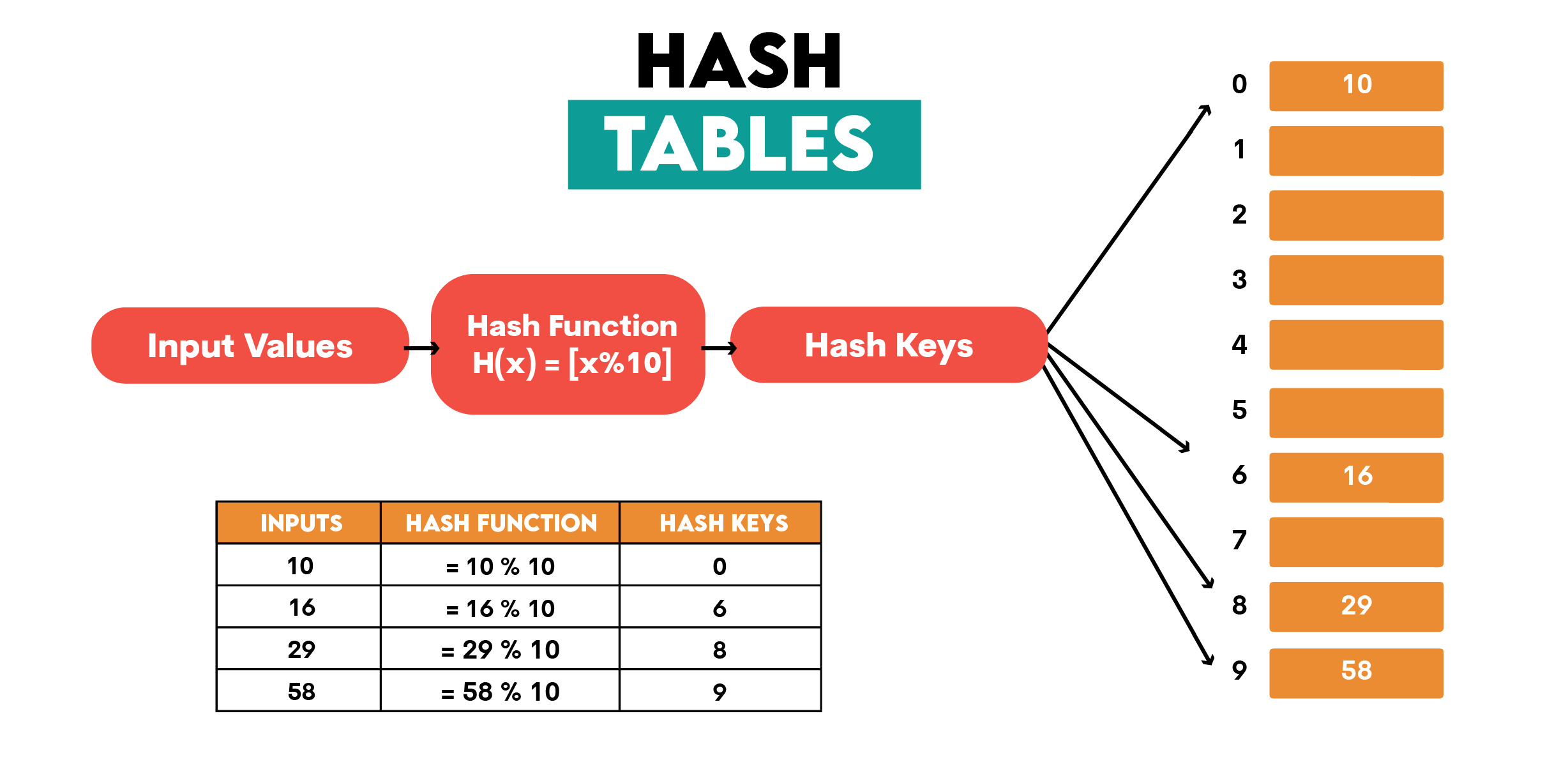
Definition: Hash tables are data structures that store key-value pairs and use a hash function to determine the index for storing elements.
Illustration:
Typical Use Examples:
- Implementing databases
- Caching data
- Storing dictionaries
Pros: Due to their design, which uses a hash function to compute an index from a key, which is then used to access the particular value directly, hash tables support high-speed data lookups. On average, the value can be accessed in constant time, O(1).
Hash tables are also memory-efficient, as they start small when implemented and resize only when the ratio of elements to table size exceeds a certain threshold.
Cons: Hash tables are susceptible to hash collisions, i.e., two or more different values being hashed to the same index. This requires special handling (e.g., chaining and open addressing), which, in turn, can degrade hash table performance.
In addition, a good hash function can minimize collisions; designing and choosing one can be challenging and time-consuming.
Data Structure Interview Questions: Hash Tables
Let’s solve the interview question by Goldman Sachs.
Given an array of integers and a positive integer k, find all distinct pairs (a,b) where b-a=k and a<b, with the pairs ordered by increasing values of a.
Link to the question: https://platform.stratascratch.com/algorithms/10433-distinct-pairs/official-solution
The question requires you to find all distinct pairs of elements whose difference equals k, given an array of integers and a positive integer.
The input data is in the form of a dictionary, which is how Python implements hash tables. In the dictionary, one key is k, which represents the specific positive difference between pairs of numbers; this is the difference we need to find. The other key is arr, which is an array of integers where we will search for these pairs of numbers.
So, we start writing the code by defining the find_pairs function that extracts the k and arr values from the input dictionary.
It then creates the count dictionary, which will be used to keep track of each number’s occurrences.
An empty set named result stores unique pairs. We chose this type of data structure because adding an already existing number pair won’t create a duplicate entry; sets handle uniqueness automatically.
The find_pairs function then iterates through each number in the array key. It checks if num + k and num - k conditions exist in count. If one or the other condition is true and the pair doesn’t already exist in the result, the pair will be added to the result.
We use (num, num + k) and (num, num - k) to ensure both possible pairs where the difference is k are captured. This is necessary because, for any given num, you might find a valid pair either by adding k to num or by subtracting k from num.
def find_pairs(input):
k = input["k"]
arr = input["arr"]
count = {}
for num in arr:
count[num] = count.get(num, 0) + 1
result = set()
for num in arr:
if num + k in count and (num, num + k) not in result and (num + k, num) not in result:
result.add((num, num + k))
if num - k in count and (num, num - k) not in result and (num - k, num) not in result:
result.add((num, num - k))
return list(result);
Run on the Test 2 input, the algorithm returns these values.
Expected Output
Official output:
[[1, 3], [3, 5], [2, 4]]Official output:
[[-8, -4], [-4, 0], [0, 4], [4, 8], [8, 12], [12, 16], [16, 20]]Official output:
[[2, 4], [4, 6]]Official output:
[]Official output:
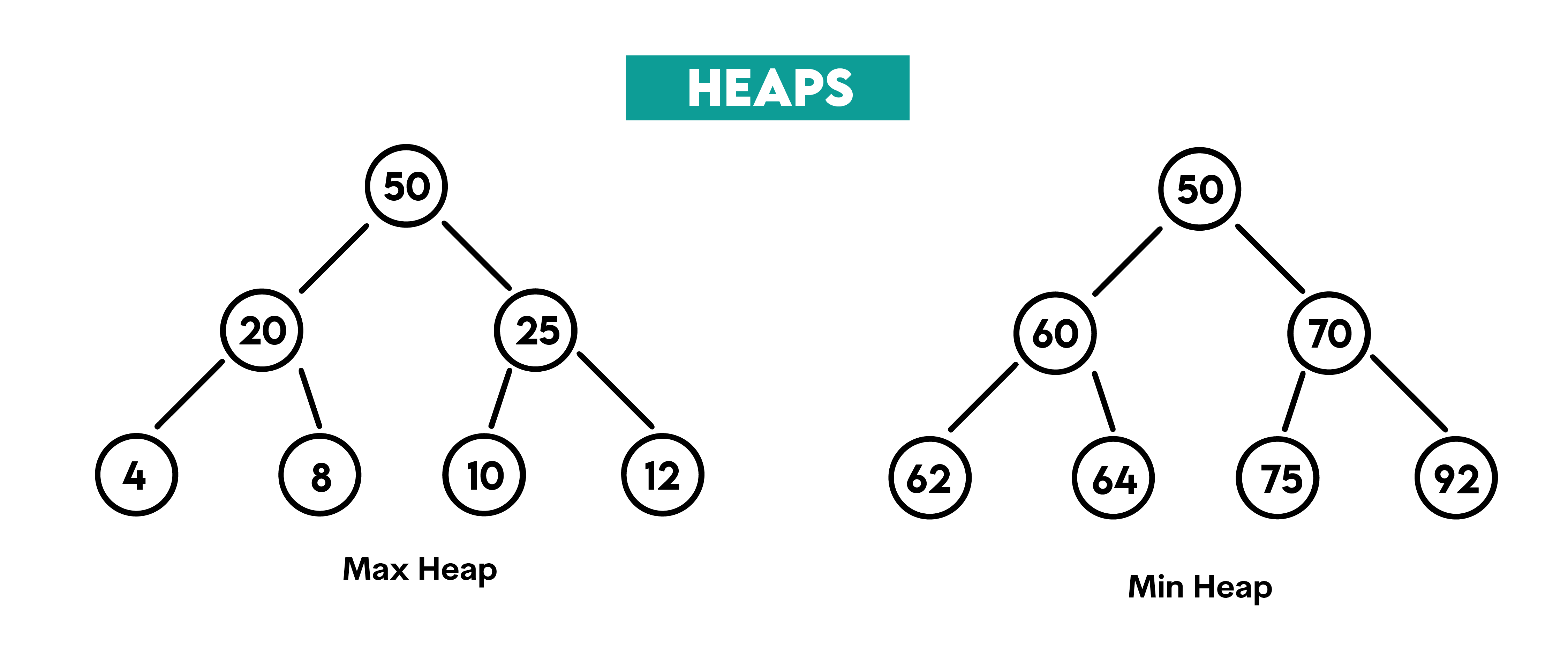
[[-5, -4], [-4, -3], [-3, -2], [-2, -1]]Heaps
Definition: Heaps are tree-based (a complete binary tree) data structures that satisfy the heap property. That property means that each parent node is
- Greater than or equal to its children, which is a max-heap
- Less than or equal to its children, which is a min-heap
Illustration:
Typical Use Examples:
- Implementing priority queues, where the highest or lowest priority element is accessed first
- Heap sort algorithm for efficient sorting
- Scheduling tasks based on priority
Pros: In heaps, the priority element is always at the root (the highest or the lowest priority), which makes them ideal for priority-based tasks; they can quickly access the maximum or minimum element with constant time being O(1).
Cons: The above characteristic also makes heaps not very suitable for searching arbitrary elements. They don’t maintain any specific order among siblings, which makes it necessary to potentially go through each element when searching.
Heaps are also relatively complex to implement and maintain compared to arrays or linked lists. This is because the heap property has to be maintained constantly, which could cause an element to ‘bubble up' through the tree (when adding an element) or ‘bubble down’ (when removing an element).
Data Structure Interview Questions: Heaps
We'll use Google and Goldman Sachs's interview question to show you how to work with heaps in practice.
Implement a method to find the maximum node value at each level of a binary tree. Write a function that returns a list of the maximum values at each level of the tree.
Link to the question: https://platform.stratascratch.com/algorithms/10392-max-nodes-in-binary-tree-levels
However, we will adapt the question a bit, so we’ll not use a binary tree, but this heap: [50, 30, 40, 10, 20, 35, 25].
In the function find_max_nodes_per_level, we define the Node class to represent each element in the heap as a node with value, left, and right attributes.
After that, we build a heap tree from our heap array. For each node in the array, the left child of a node at index i is at index 2*i +1, and the right child is at index 2*1+2.
Then, the function find_max_nodes operates on the tree we constructed, traversing it level by level and finding and storing the maximum node value at each level.
The root of the tree is returned by build_heap_tree and passed to find_max_nodes to determine the maximum values at each level.
def find_max_nodes_per_level(heap_values):
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
def build_heap_tree(values):
if not values:
return None
nodes = [None if val is None else Node(val) for val in values]
n = len(values)
for i in range(n):
left_index = 2 * i + 1
right_index = 2 * i + 2
if left_index < n:
nodes[i].left = nodes[left_index]
if right_index < n:
nodes[i].right = nodes[right_index]
return nodes[0]
def find_max_nodes(root):
if root is None:
return []
max_nodes = []
queue = [root]
while queue:
level_max = float('-inf')
level_size = len(queue)
for _ in range(level_size):
node = queue.pop(0)
level_max = max(level_max, node.value)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
max_nodes.append(level_max)
return max_nodes
root = build_heap_tree(heap_values)
return find_max_nodes(root);
Conclusion
Data structures are an essential stepping stone for understanding and working with algorithms. In this article, we covered several of the most common data structures:
- Arrays
- Strings
- Linked Lists
- Stacks
- Queues
- Trees
- Graphs
- Hash Tables
- Heaps
Their importance is exemplified in data structure interview questions, which are a common feature in technical job interviews.
These interviews revolve around coding, which is also the best way to practice data structure interview questions. In particular, you can achieve that by solving algorithm questions involving diverse data structures.
Share


